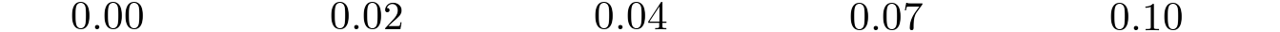Adversarial Generation of Continuous Implicit Shape Representations
This article provides an overview of the paper "Adversarial Generation of Continuous Implicit Shape Representations", which I co-authored with Matthias Fey. While the paper focuses on the theoretical aspects, I'll provide a higher level explanation and and some visualizations here on the blog.
In the paper, we propose a GAN that generates 3D shapes. The GAN uses a DeepSDF network as a generator and either a 3D CNN or a Pointnet as the discriminator.
Update June 2020: Here is a recording of the presentation I gave about the paper at the virtual Eurographics 2020 conference.
DeepSDF
First, I'll introduce the idea behind DeepSDF. The standard way of representing 3D shapes in deep learning models uses voxel volumes. They are a generalization of images to 3D space and and use voxels instead of pixels. With this 3D CNN approach, concepts from deep learning for images can be applied to 3D shapes.
However, CNNs are well suited for learning texture properties and learning to represent a 3D shape as a combination of 3D texture patches is not ideal. Furthermore, due to the memory requirements of this approach, high voxel resolutions are not feasible.
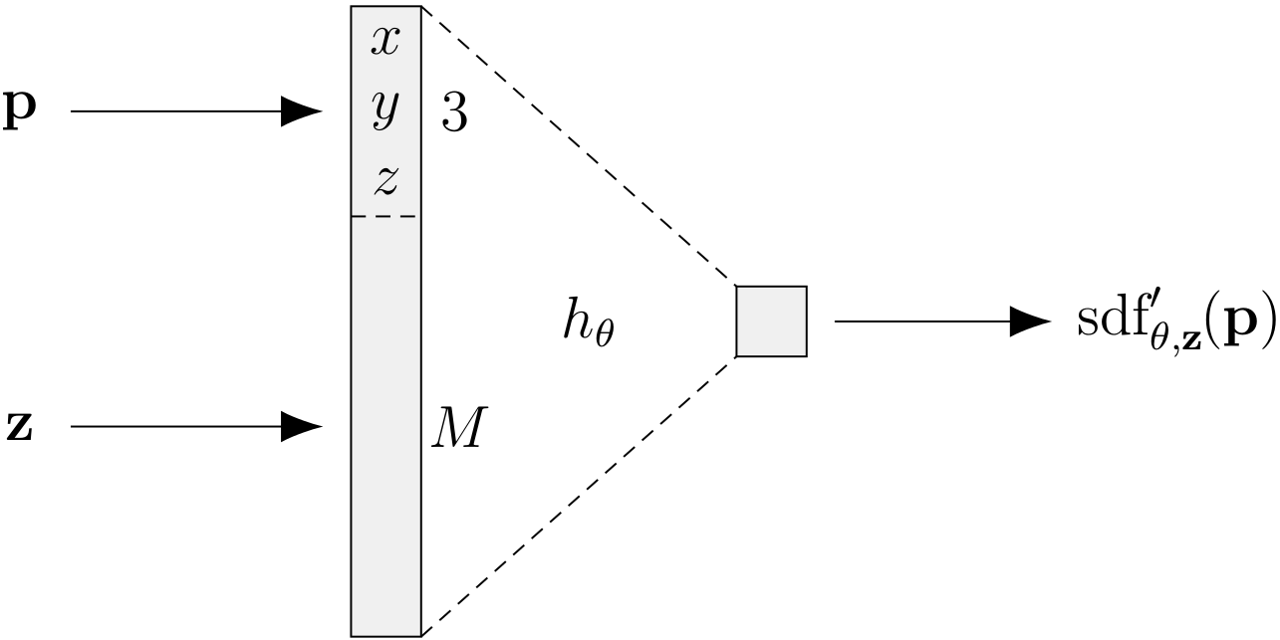
A voxel volume contains a rasterized representation of the signed distance field of the shape. The signed distance function is a function that maps a point in 3D space to a scalar signed distance value. The idea behind the DeepSDF network is to train a neural network to predict the value of the signed distance directly for an arbitrary point in space. Thus, the network learns a continuous representation instead of a rasterized one. An SDF network for a single shape has three input neurons and one output neuron. The DeepSDF network doesn't use convolutions.
To learn a representation of multiple shapes, the DeepSDF network receives a latent code as an additional input.
The decision boundary of the network is the surface of the learned shape. For a given latent code, a mesh can be created using Marching Cubes by evaluating the network for a raster of points. The resolution of that raster can be selected arbitrarily after the network was trained.
The DeepSDF network is trained on a dataset of 3D points with corresponding SDF values. These points are in part uniformly sampled and in part normally distributed around the shape surface, resulting in a high density of training data near the surface.
Generating SDF data for the ShapeNet dataset is quite challenging because the dataset contains non-watertight meshes. I made my own implementation of the approach proposed in the DeepSDF paper, as well as a slightly different approach. I published this project as a python module.
I created my own implementation of the DeepSDF network and trained it on the ShapeNet dataset. The DeepSDF autodecoder works like an autoencoder, but without the encoder. The latent codes are assigned randomly and then optimized during training using SGD.
In the animation above, you see a t-SNE plot of the learned latent space of the DeepSDF autodecoder for the ShapeNet dataset. The colors show dataset categories which are not known to the network. It has learned on its own to assign similar latent codes to shapes of the same category. The shapes on the left are reconstructions of latent codes along a random spline path through the latent space. Click here for a high resolution version of the animation.
GAN
So far, I introduced the DeepSDF autodecoder that learns to reconstruct a given dataset of shapes. The contribution of our paper is to propose a GAN architecture that trains a DeepSDF network to generate new shapes.
A generative adversarial network is a pair of a generator network and a discriminator network. The generator proposes new samples (in our case shapes) and the discriminator predicts whether a given sample was generated by the generator ("fake") or taken from the dataset ("real"). The trick is that the generator is improved using the gradient of the discriminator output and the discriminator is trained on the dataset of real samples and the increasingly realistic fake samples provided by the generator. Thus, the generator and discriminator have adversarial goals. If the GAN training is successful, the GAN reaches an equilibrium where the generator has learned a mapping from the latent distribution to the underlying distribution of the dataset and discriminator assesses generated and real samples with the same score.
3D GANs based on 3D CNNs have been proposed. Our research question was whether a GAN can be trained where the generator uses the DeepSDF architecture.
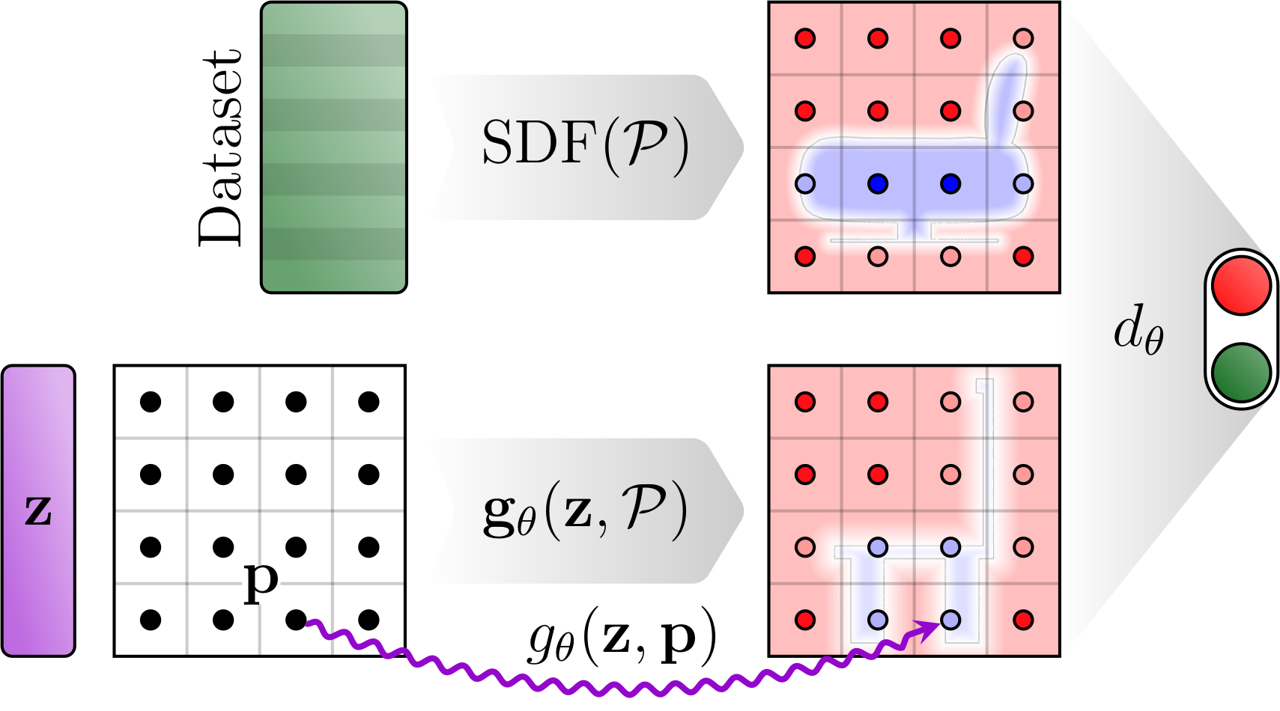
Usually, the discriminator of the GAN is a mirrored version of the generator. In the case of the DeepSDF network, this is not feasible because a single sample of the DeepSDF network provides only the SDF for one point. From one point alone, a discriminator could not assess if the sample is realistic. Instead, the discriminator needs multiple points to judge the output value in context.
Voxel discriminator
One solution to the problem of missing context is to use a 3D CNN as the discriminator. In this case, the generator is evaluated for a batch of raster points and the resulting SDF values are rearranged into a voxel volume. The idea to combine a continuous implicit shape network with a 3D CNN was proposed by Chen and Zhang for their autoencoder.
The training data for the voxel discriminator are voxel volumes. We use datasets with resolution 8³, 16³, 32³ and 64³ and apply progressive growing. We use the Wasserstein distance with gradient penalty (WGAN-GP).
Here is a latent space interpolation of shapes generated with the voxel discriminator:
Another interesting observation is the generator's ability to generalize from the raster points to intermediate points that it was not trained on. Here is an example of a network that was only trained on 16^3 voxels (!), which is the first stage of the progressive growing.
On the left, the shapes were reconstructed with 16^3 raster points (the same resolution it was trained on). Scaling up the resolution linearly makes it smoother, but doesn't add any detail. When querying the network at 128^3, we see that the network is able to generalize to higher resolutions. For some parts of the geometry, the low resolution volume has no sample points with negative values, resulting in apparently missing geometry. In these cases, the network still generates negative SDFs for intermediate points, thus making the geometry appear when sampled at a higher resolution.
Pointnet discriminator
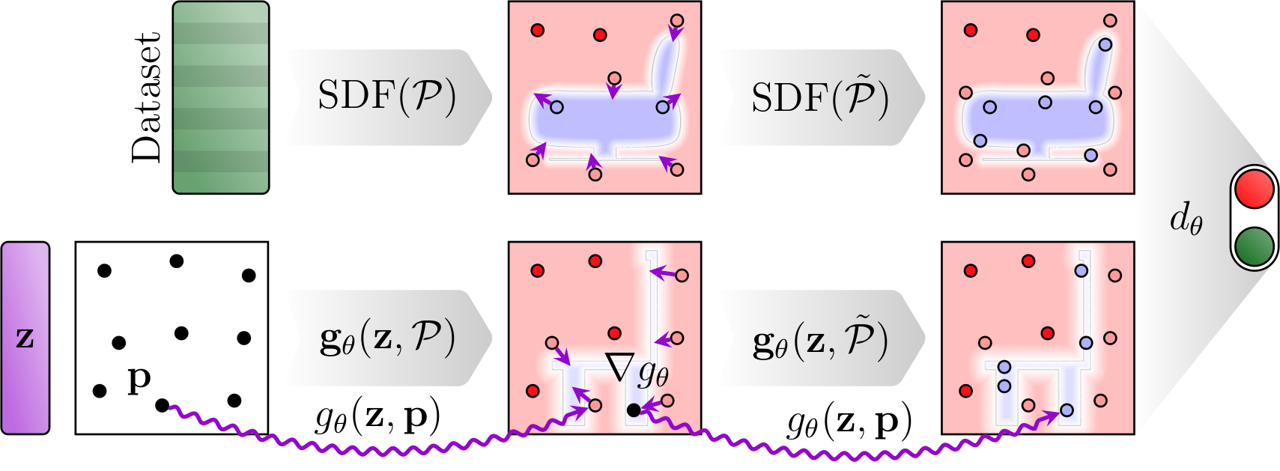
Since the voxel-based discriminator keeps some of the disadvantages of fully voxel-based GANs, we investigated an approach that doesn't use voxels at all. The Pointnet is a neural network architecture that can operate on point clouds. In our case, we sample a point cloud of uniform points and use the generator to predict SDFs for the points. The Pointnet then receives the positions of the points and the signed distance values as a "feature vector" with one element. This way, we avoid the fixed raster points and use always changing query points. A Pointnet typically infers information from the spatial structure of the points, which in our case is random. Regardless, we found that the Pointnet can be used as the discriminator in our case.
To train the GAN with the Pointnet discriminator, we use a ground truth dataset of uniformly sampled points with their corresponding SDFs. We "grow" the point clouds during training simply by increasing the number of points.
When the surface of the generated SDF is reconstructed using Marching Cubes, only values close to sign changes matter. We would like the network to spend more model capacity on values close to the surface, as they influence the result the most. We achieved that by refining the network with additional sample points close to the surface. The gradient of the SDF gives us the direction towards the shape's surface and for a neural network the gradient is easily computed. Using that, we can move randomly sampled points closer to the surface of the generated shape. The non-uniform point cloud can then be evaluated by the discriminator. Since the Pointnet takes the positions of the points into account, it could discern a uniformly sampled point cloud from a surface point cloud. Thus, we add surface points to the ground truth data as well.
Here are some examples of shapes generated with the Pointnet discriminator and uniformly sampled points (top) and shapes generated with the refinement method (bottom). (I'll replace this with an animated version soon.)
For both approaches, we found a surprising result when trying different levels for Marching Cubes. By default, Marching Cubes reconstructs the isosurface at the level 0, i.e. the surface where the predicted SDF is zero. However, we can choose another level, effectively eroding or dilating the shape. We would expect that the ideal level would be 0, since that is the isosurface of the training data. However, when experimenting with different values, we observe that some features appear to be missing at level 0.
We chose an isosurface level of 0.04 to reduce missing geometry at the cost of slightly rounded corners. Since we clip the ground truth SDF at -0.1 and 0.1, the isosurfaces of generated SDF outside of that range are not usable.